Image Alignment

Image Alignment

1. Template matching

   Slow, combinatory, global solution

2. Multi-scale template matching

   Faster, combinatory, locally optimal

3. Local refinement based on some initial guess

   Fastest, locally optimal

Translation: $\begin{bmatrix}x+p_1 \\ y + p_2\end{bmatrix} = \begin{bmatrix}1 & 0 & p_1 \\ 0 & 1 & p_2\end{bmatrix} * \begin{bmatrix}x \\ y \\ 1\end{bmatrix}$

Affine: $\begin{bmatrix}p_1x+p_2y+p_3 \\ p_4x+p_5y+p_6\end{bmatrix} = \begin{bmatrix}p_1 & p_2 & p_3 \\ p_4 & p_5 & p_6\end{bmatrix} * \begin{bmatrix}x \\ y \\ 1\end{bmatrix}$

Definition of Image Alignment Problem

$min_p\sum[I(W(x;p))-T(x)]^2$

$W(x;p):$ warped image

$T(x):$ template image

$p:$ transformation parameters

Warp parameters $p$ such that the SSD is minimized over all the pixels in the template image

Strategy: assume a good initial guess for $p$ and linearize the objective function so that we can do incremental updates (basically gradient descent)

Lucas-Kanade Alignment

Assumption: good initial guess of $p$, $\Delta p$ is small

$\sum_x[I(W(x;p))-T(x)]^2 \rightarrow \sum_x[I(W(x;p+\Delta p))-T(x)]^2$

Strategy: linearize $I()$, e.g. with Taylor series approximation perhaps this is okay for a very small increment $\Delta p$

$I(W(x;p+\Delta p)) \approx I(W(x;p)) + {\delta I(W(x;p)) \over \delta p}\Delta p$

$=I(W(x;p))+{\delta I(W(x;p))\over \delta x’}{\delta W(x;p) \over \delta p}\Delta p$

$=I(W(x;p))+\nabla I {\delta W\over \delta p}\Delta p$

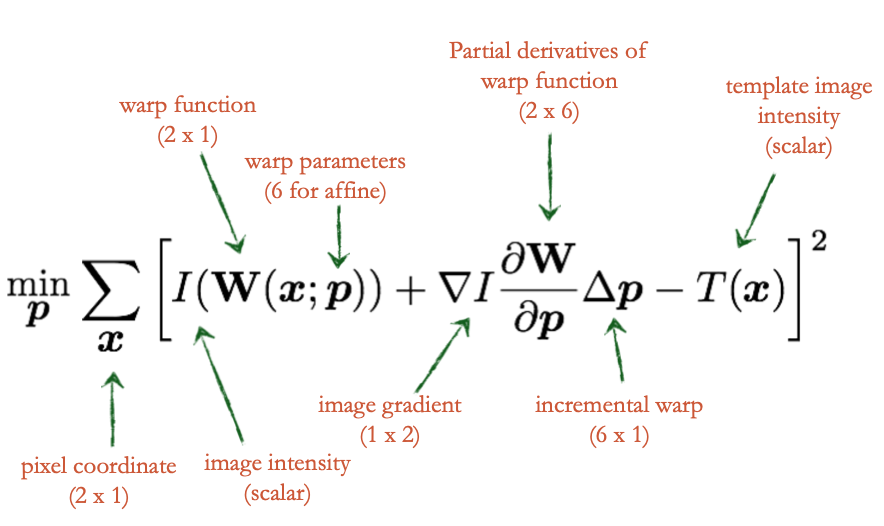
Implementation-wise, we should compute in parallel.

Solving LK Algo

$\sum_x[I(W(x;p+\Delta p))-T(x)]^2 \rightarrow \sum_x[I(W(x;p))+\nabla I {\delta W \over \delta p}\Delta p - T(x)]$

$\rightarrow \sum_x[\nabla I {\delta W \over \delta p}\Delta p - (T(x)-I(W(x;p)))]^2$

$\Delta p = H^{-1}\sum_x[\nabla I {\delta W \over \delta p}]^T[T(x)-I(W(x;p))]$ where $H=\sum_x[\nabla I {\delta W \over \delta p}]^T[\nabla I {\delta W \over \delta p}]$

For successful inversion, H should be well-conditioned, i.e. eigenvalues are both large and approx. similar in magnitude $\rightarrow$ corner region

Kanade-Lucas-Tomasi Tracker

How to Choose Good Features for Tracking?

Hessian of gradients should be well-conditioned, both eigenvalues sufficiently large, i.e. a corner

KLT Algorithm

1. Find corners satisfying $min(\lambda_1, \lambda_2)>\lambda$

2. Loop over corners
   • For each corner compute displacement to next frame using the Lucas-Kanade alignment method
   • Store displacement of each corner, update corner position
   • (optional) Add more corner points every M frames using 1
3. Returns long trajectories for each corner point

Challenges of Feature-Based Tracking

• Figuring out which features can be tracked
• How to track them efficiently
• Changing appearance of some points e.g. rotations, movement into shadows, etc.
• Drift: accumulation of small errors as appearance model updates
• Appearance/disappearance of points (how to handle the addition and removal of tracked points)

Feature Tracking vs Optical Flow

Mean-shift Tracking

1. Compute a descriptor for the target

2. Search for similar descriptor in neighborhood in next frame with mean shift
3. Most similar candidate gets reassigned as target, repeat