Yang Shuqi

Kadane's Algorithms

 

    Features

    • Find the largest contiguous elements in an array
    • O(n)
    • Dynamic Programming

    Explaination

    Assume we’re finding the largest contiguous elements Maximum in an array A

    1. Optimization The largest contiguous elements S[i] in A that ends exactly with A[i] is S[i]= Max(S[i-1]+A[i], A[i-1]) i.e. the maximum of the largest contiguous elements S[i-1] in A that ends exactly with A[i-1] plus A[i] or A[i] itself (i.e. S[i-1] < 0 and thus is given up)
    2. To find the largest contiguous elements S in an array A, computes S for each element in A, the largest of them is what we want.

    2-D Version

    Find the largest contiguous rectangles in a 2-D array

    Assume the following is the array we need to process

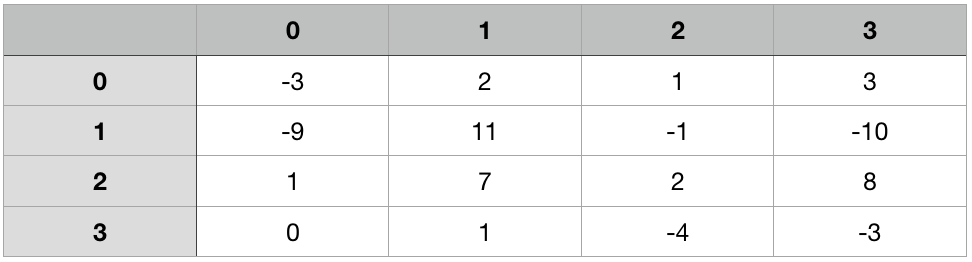
    Original Array

    Enumerate through the rows. For each pair of row_i to row_j, we compute prefix sum for each column. And then apply Kadane’s Algorithm to the result 1-D array.

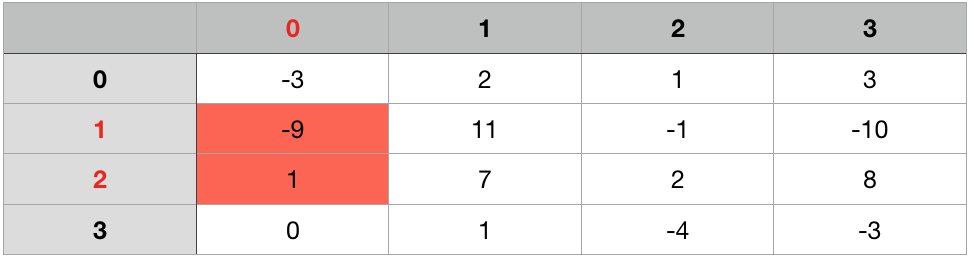
    Step a

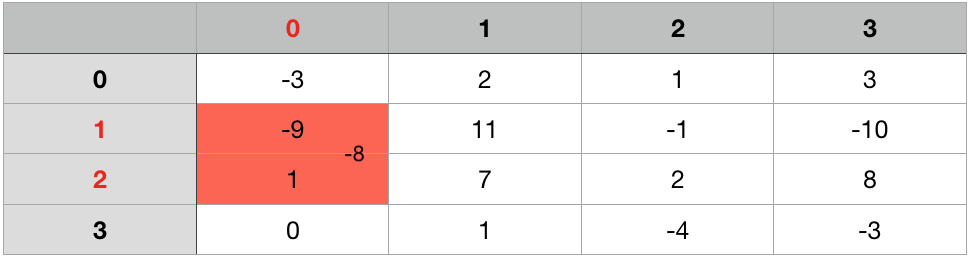
    Step b

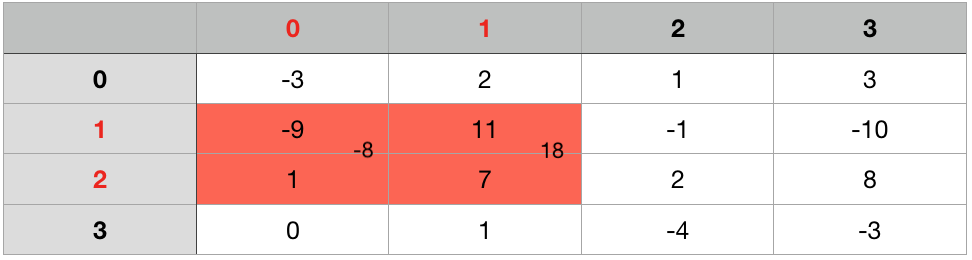
    Step d

    Step e

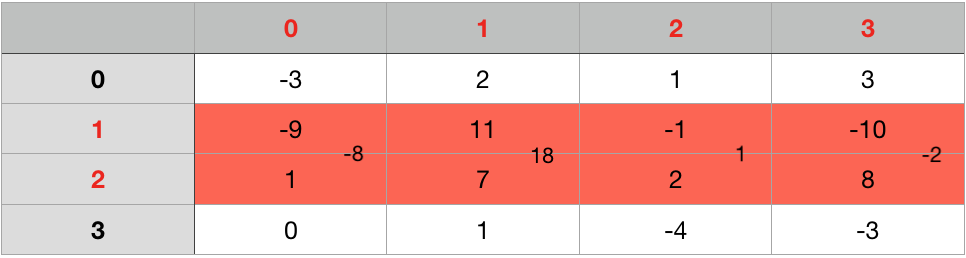
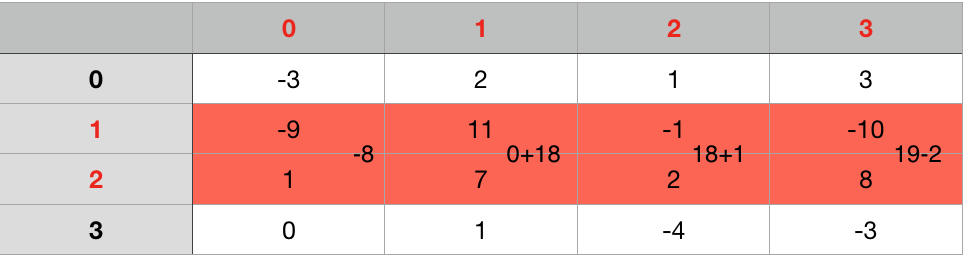
    Step f

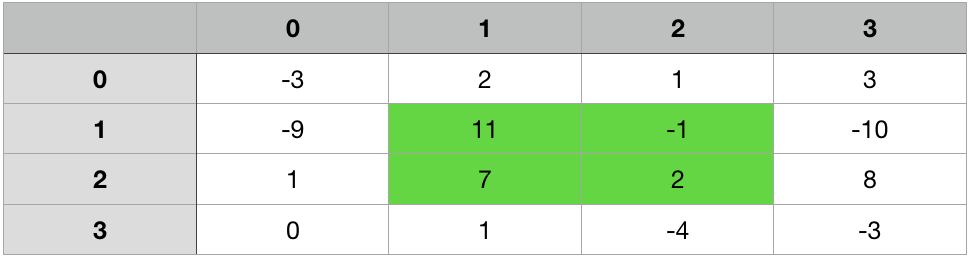
    Step g

    2-D Version with K

    Find the largest contiguous rectangles in a 2-D array which doesn’t exceed K

    Instead of applying Kadane’s Algorithm, we need to compute prefix sum of the 1-D array that ends with col_d now.

    Step 1

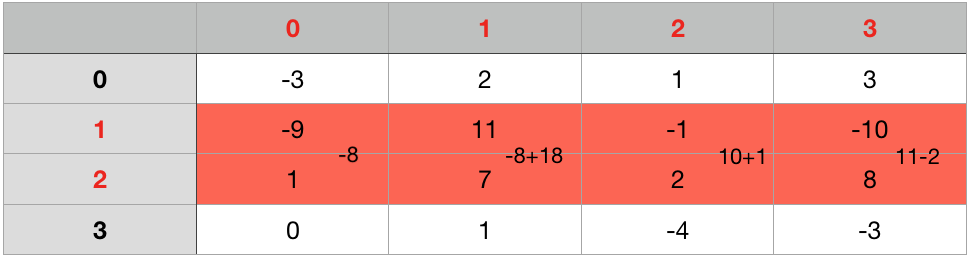
    Step 2

    Find M = ceil(S-K) to find the smallest sub-rectangle to be eliminated. S - M is the result.

    Search