Projection from 3D to 2D lost information
- length
- angles
- scale (cannot be recovered)
- Why?
Euclidean vs. Projective Geometry
Projective Geometry
Lost: Angles, distance, ratio of distances
Preserved: straightness
We study of geometric properties that are invariant wrt projective transformations in projective geometry.
Euclidean Geometry
No formal representation of infinity
Homogeneous coordinates
Points: $(x, y, k)^T$
$(x, y, k)$ where $k = 0$ represents point at infinity / ideal point.
Dof: 2 $(x, y)$
Lines: $k(a, b, c)^T$
A line in the plane is represented by: $ax+by+c=0$
$(0,0,0)^T$ doesn’t correspond to any line.
$(0, 0 , 1)^T$ represents line at infinity.
Dof: 2 $(a: b: c)$
Point $x$ Lies on Line $l$: $x^Tl=l^Tx=0$
Ideal points lines on line at infinity. $(0, 0, 1) (x_1, x_2, 0)^T = 0$
Intersection of Lines: $x=l \times l’$
The intersection point is $(b, -a, 0)^T$ represents that these two lines are parallel.
$(b, -a)^T$ represents the line’s direction.
The line at infinity can be thought of as the set of directions of lines in the place.
Line Joining Points: $l = x \times x’$
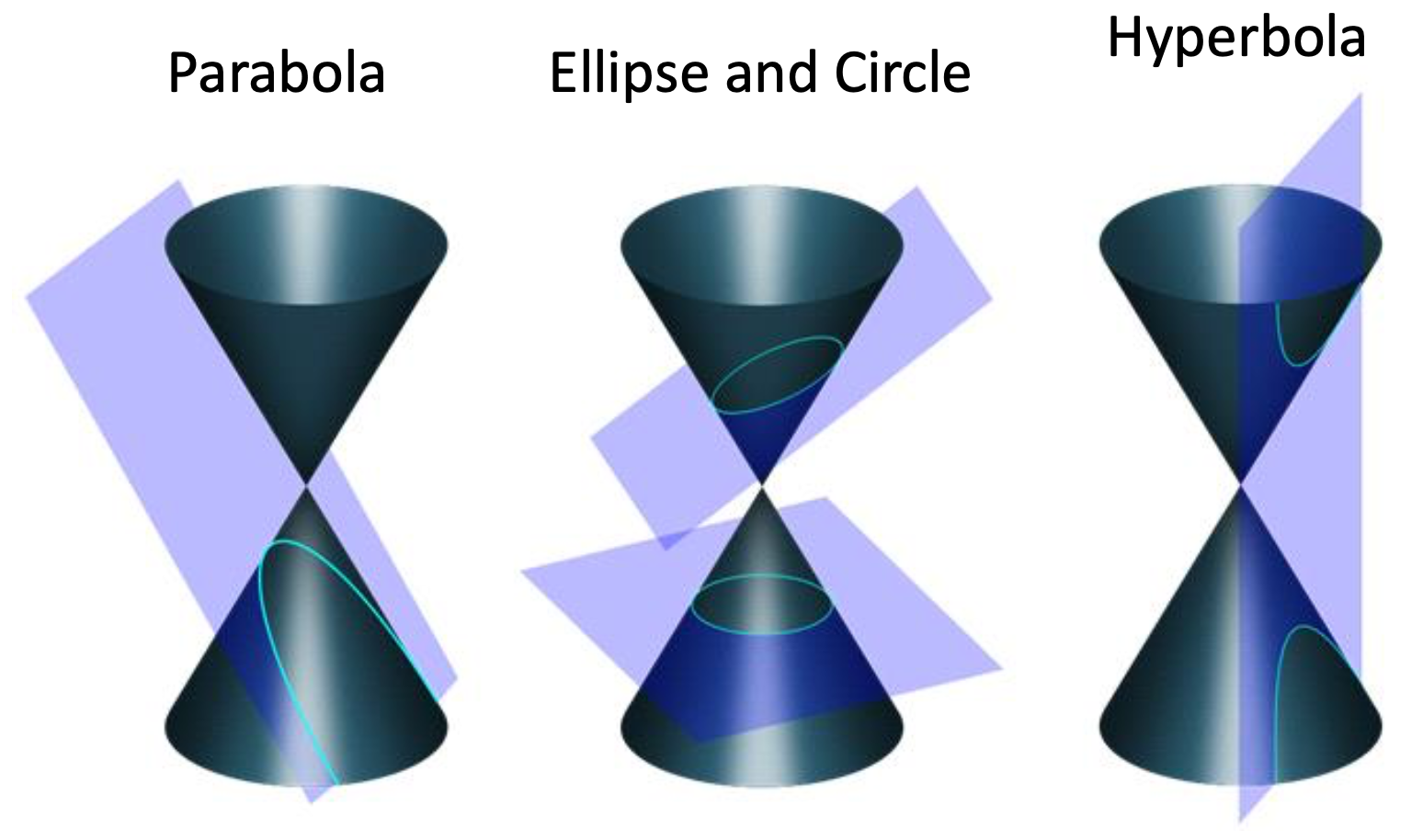
Conics
A curve describe by a second-degree equation in the plane: hyperbola, ellipse, and parabola.
$ax^2+bxy+cy^2+dx+cy+f=ax_1^2+bx_1x_2+cx_2^2+dx_1x_3+ex_2x_3+fx_3^2=0$
$x^TCx=0$ where $C = \begin{bmatrix} a & b/2 & d/2 \ b/2 & c & e/2 \ d/2 & e/2 & f\end{bmatrix}$
Dof: 5 $(a: b: c: d: e: f)$
Each point places one constraint $\rightarrow$ 5 points can uniquely determine a conic.
Tangent Lines to Conics: $l=Cx$
Points Lie on Conic: $x^TCx=0$
Dual Conics
A line $l$ tangent to $C$ satisfies $l^TC^*l=0$.
For a non-singular symmetrix matrix $C*=C^{-1}$
Dof: 5
5 lines can uniquely determine a dual conic.
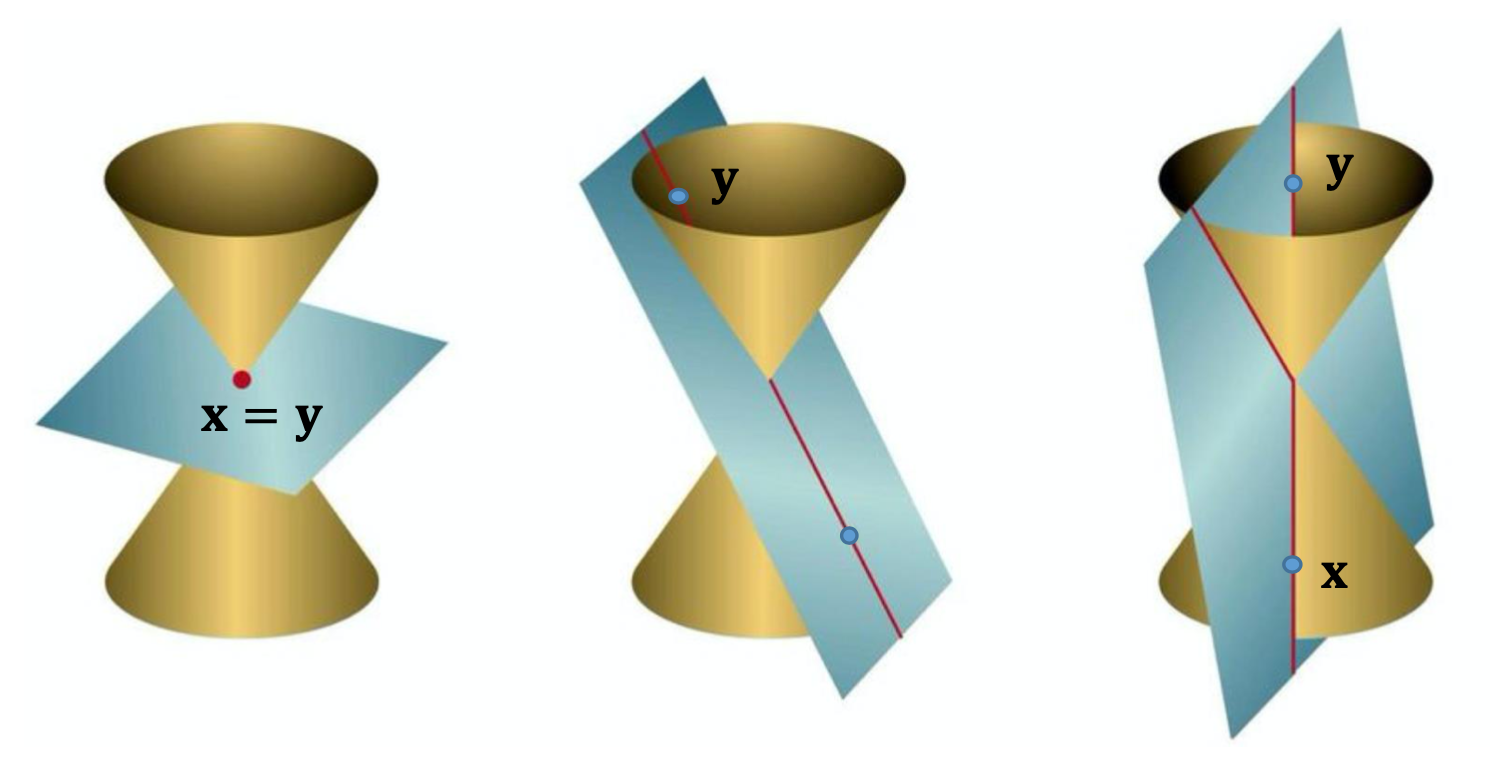
Degenerate Conics $(x+\alpha y)^TC(x+\alpha y)=0$
$l=Cx=Cy$ and $l^Ty = l^Tx = 0$
$rank(C) < 3$, i.e. not of full rank
The matrix is not invertible, therefore $(C^)^=C$
Hierarchy of Transformation
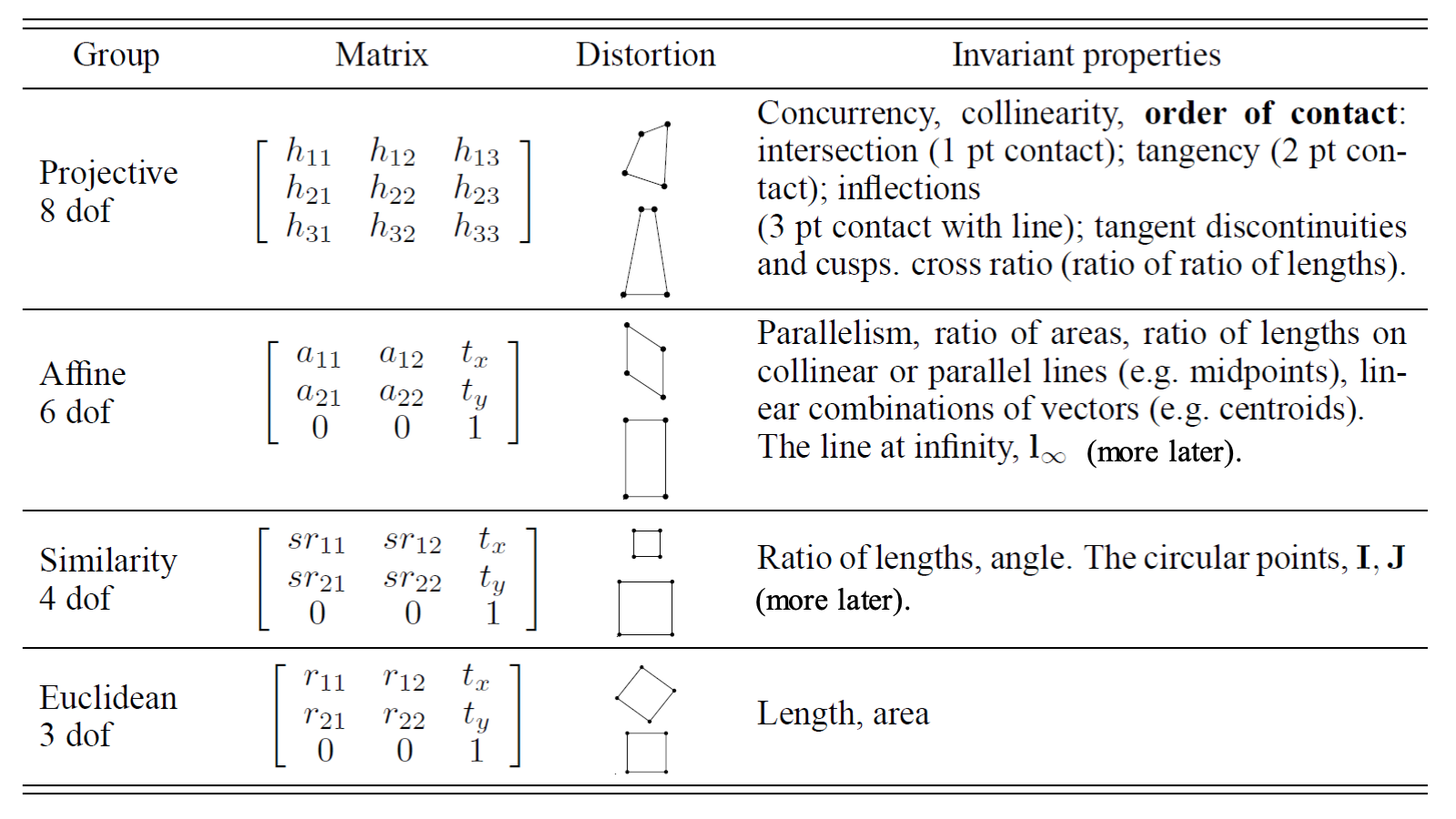
Properties of H
- Non-singular 3x3 matrix
- Homogeneour matrix since only the ratio of the matrix elements is significant
- 8 Dof
The points $Hx$ all lies on the line $H^{-T}l$
Points: $x’=Hx$
Lines: $l’=H^{-T}l, l’^T=l^TH^{-1}$
Conics: $C’=H^{-T}CH^{-1}, C^{}{‘}=H^{-T}C^H^{-1}$
Isometry: preserve Euclidean distance
$H_E = \begin{bmatrix} \epsilon \cos\theta & -\sin \theta & t_x \ \epsilon \sin \theta & \cos \theta & t_y \ 0 & 0 & 1\end{bmatrix}$, where $\epsilon=\pm1$
Invariants: length, angle, area
Similarity / Equiform: isometry + isotropic scaling
$H_S = \begin{bmatrix} s \cos\theta & -s\sin \theta & t_x \ s \sin \theta & s\cos \theta & t_y \ 0 & 0 & 1\end{bmatrix}$, where $s$ represents the isotropic scaling
Dof: 4 (3 isometry + 1 scale)
Can be computed from 2 point correspondences.
Invariants: ratio of two lengths, angle, ratio of areas
Affine
$H_A = \begin{bmatrix} a_{11} & a_{12} & t_x \ a_{21} & a_{22} & t_y \ 0 & 0 & 1\end{bmatrix}$, where $A$ is a 2x2 non-singular matrix.
Dof: 6
Can be computed from 3 point correspondences.
Invariants: parallel lines, ratio of lengths of parallel line segments, ratio of areas
$A = R(\theta)R(-\phi)DR(\phi)$, where $R(\theta)$ and $R(\phi)$ are rotations by $\theta$ and $\phi$ respectively, and $D = \begin{bmatrix}\lambda_1 & 0 \ 0 & \lambda_2\end{bmatrix}$
Projective
$H_P = \begin{bmatrix} a_{11} & a_{12} & t_x \ a_{21} & a_{22} & t_y \ v_1 & v_2 & v\end{bmatrix}$, where $v$ can be $0$
Dof: 8
Can be computed from 4 point correspondences, with no three collinear on either plane.
Invariants: order of contact, tangency (2 point contact), cross ratio
Decomposition of a Projective Transformation
Valid provided $v ≠ 0$
Unique if $s$ is chosen positive

A: non-sigular matrix given by $A=sRK+tv^T$
K: upper-triangular matrix matrix normalized as $det(K)=1$
Cross Ratio
| $Cross(\bar{x_1}, \bar{x_2}, \bar{x_3}, \bar{x_4}) = { | \bar{x_1}\bar{x_2} | \bar{x_3}\bar{x_4} | \over | \bar{x_1}\bar{x_3} | \bar{x_2}\bar{x_4} | }$, where $ | \bar{x_i}\bar{x_j} | = det {\begin{bmatrix} x_{i1} & x_{j1} \ x_{i2} & x_{j2} \end{bmatrix}}$ |
-
If each point $\bar{x_i}$ is a finite point and $x_2=1$, then $ \bar{x_i}\bar{x_j} $ represents the signed distance from $\bar{x_i}$ to $\bar{x_j}$. - Also valid if one of the points $\bar{x_i}$ is an ideal point.
Concurrent Lines
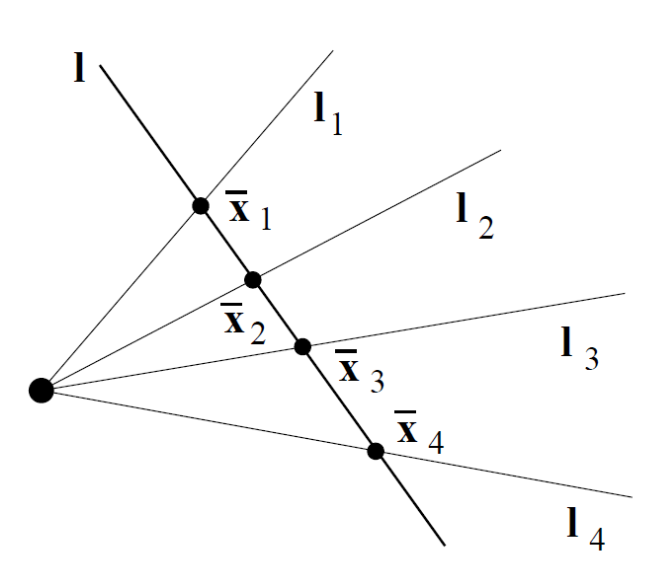
Four concurrent lines $l_i$ intersect the line $l$ in the four points $\bar{x_i}$.
Projective Geometry and Transformations of 3D
Point: $(X_1, X_2, X_3, X_4)^T$
$X’ = HX$
Plane: $(\pi_1, \pi_2, \pi_3, \pi_4)^T$
$\pi’=H^{-T}\pi$
Plane Normal: $n = (\pi_1, \pi_2, \pi_3)^T$
Dof: 3 $(\pi_1: \pi_2: \pi_3: \pi_4)$
Point on Plane: $\pi^TX=0$
Inhomogenour notation: $n\bar{X}+d=0$, where $\bar{X}=(X, Y, Z)^T, X_4 = 1$ and $d = \pi_4$
| Distance of the plane from the origin: $d/ | n | $ |
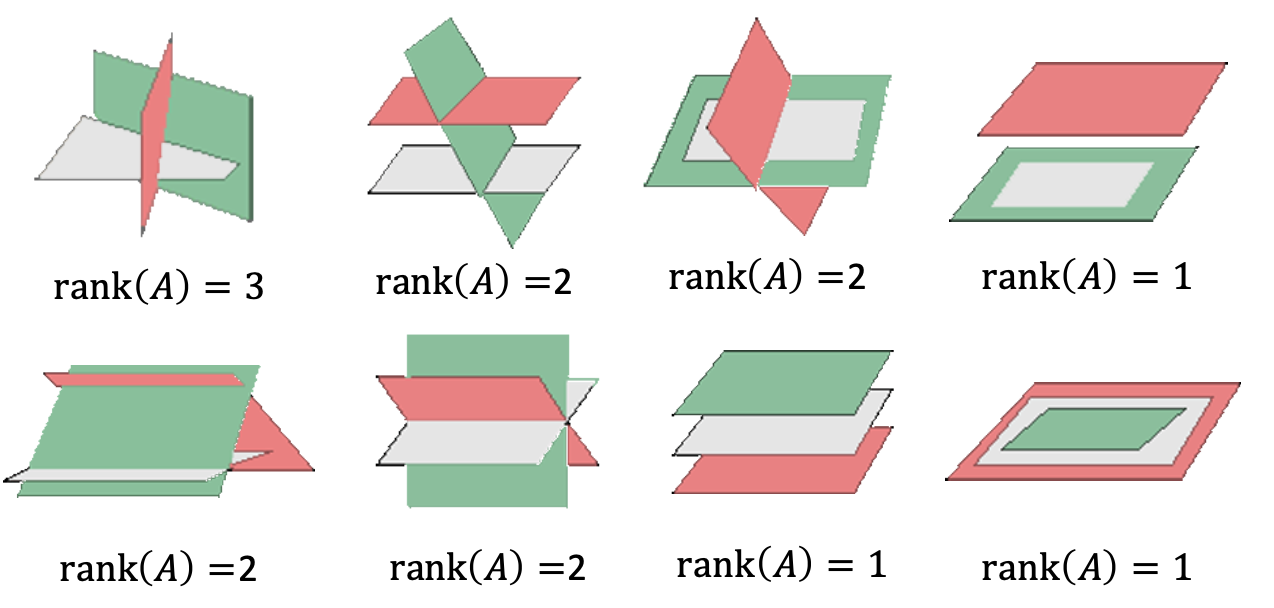
Three Points Define a Plane
$(X_1^T, X_2^T, X_3^T)^T\pi=0$
Rank = 3 when the points are linearly independent $\rightarrow$ a plane
Rank = 2 when the points are collinear $\rightarrow$ a pencil of planes with the line of collinear points as axis
Three Planes Define a Point
$(\pi_1^T, \pi_2^T, \pi_3^T)^TX=0$
Parametrized Points on a Plane
$X = M_{4\times3}x$, where $\pi^TM=0$ and the 3-vector $x$ parametrized points on the plane $\pi$
$M$ is not unique
| Suppose $\pi = (a, b, c, d)^T$ and $a≠0$, $M^T = [p | I_{3 \times 3}]$, $p = (-{b \over a}, -{c \over a}, -{d \over a})^T$ |
Line
Dof: 4
Null space and span representation
- 2 points: $W=\begin{bmatrix}A^T \ B^T\end{bmatrix}$
- The span of $W^T$ is the pencil of points
- The span of the 2-dimensional right null-space of $W$ is the pencil of planes with the line as axis
- Independent of the particular points used to define it
- 2 planes: $W^* = \begin{bmatrix}P^T \ Q^T\end{bmatrix}$
- The span of $W^{*T}$ is the pencil of planes with the line as axis
- The span of the 2-dimensional right null-space of $W^*$ is the pencil of points on the line
$W^W^T = WW^{T}=0_{2\times2}$
- point + line: $M = \begin{bmatrix}W \ X^T\end{bmatrix}$
- If the null-space of $M$ is 2-dimensional then $X$ is on $W$, otherwise $M\pi=0$
- line + plane: $M = \begin{bmatrix}W^* \ \pi^T\end{bmatrix}$
- If the null-space of $M$ is 2-dimensional then the line $W$ is on $\pi$, otherwise $MX=0$
Plucker Matrices
The line joining the two points $A$ and $B$ is represented by the 4x4 skew-symmetric homogeneous: $L=AB^T-BA^T$, with elements $l_{ij}=A_iB_j-B_iA_j$
$A=(A_1, A_2, A_3, A_4)^T=(w, x, y, z)^T$
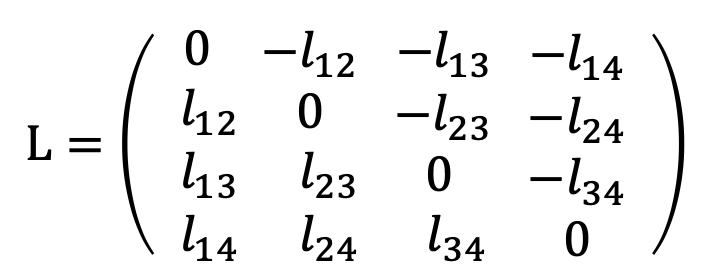
Plucker line: $\mathcal{L}={l_{12}, l_{13}, l_{14}, l_{23}, l_{42}, l_{34}}$
6 non-zero elements
direction vector: $d=B-A=(l_{12}, l_{13}, l_{14})$
moment vector: $m = A \times B =(l_{23}, l_{42}, l_{34})$
$det(L)=0 \rightarrow l_{12}l_{34}-l_{13}l_{42}+l_{14}l_{23}=0$
Several Properties of L
-
$Rank(L) = 2$, its 2-dimensional null-space is spanned by the pencil of planes with the line as axis.
$LW^{*T}=0_{4 \times 2}$
-
The representation has the required 4 dof for a line.
5 ratios - 1 for $det(L)=0$
-
$X’=HX \rightarrow L’=HLH^T$
-
It’s generalization to 4-space of the vector product formula $l=x\times y$
-
It’s independent of the points $A, B$ used to define it.
Dual Plucker Matrices
A dual Plucker representation $L^$ is obtained for a line formed by the intersection of two planes $P, Q$: $L^=PQ^T-QP^T$
-
$X’=HX \rightarrow L^*=H^{-T}LH^{-1}$
-
$l_{12}:l_{13}:l_{14}:l_{23}:l_{42}:l_{34} = l_{34}^:l_{42}^:l_{23}^:l_{14}^:l_{13}^:l_{12}^$
Plane Defined by Point and Line: $\pi=L^*X$
$L^*X=0$ iff $X$ is on $L$
Point Defined by Line and Plane: $X=L\pi$
$L\pi=0$ iff $L$ is on $\pi$
Intersection of Two Lines:
| $det[A, B, A’, B’] = (\mathcal{L} | \mathcal{L’})=0$ |
| $det[P, Q, P’, Q’] = (\mathcal{L} | \mathcal{L’})=0$ |
| $(P^TA)(Q^TB)-(Q^TA)(P^TB)=(\mathcal{L} | \mathcal{L’})=0$ |
Quadrics: $X^TQX=0$
$Q$ is a symmetric 4x4 matrix
$X’=HX \rightarrow Q’=H^{-T}QH^{-1}$
Dof: 9 = 10 elements - 1 for scale
Nine points in general position define a quadric
If the matrix $Q$ is singular, then the quadric is degenerate, and may be defined by fewer points.
Dual Quadrics: $\pi^TQ^*\pi=0$
$Q^*=adjointQ$ or $Q^{-1}$ if $Q$ is invertible
$X’=HX \rightarrow Q^{‘}=HQ^H^T$
Conic: $C=M^TQM$
$X^TQX=x^TM^TQMx=x^TCx$