Affine Rectification: remove projective distortion
The image of $l_{\infin}$ is specified
$l_{\infin}$ is a fixed line under affine transformation, i.e. $H_{31} = H_{32} = 0$
In general, under an affinity, a point on $l_{\infin}$ is mapped to another point on $l_{\infin}$
$H_p’ = H_AH_P^{-1} =H_A\begin{bmatrix}1 & 0 & l_1 \ 0 & 1 & l_2 \ 0 & 0 & l_3 \end{bmatrix}$, where $H_A$ can be any affinity transformation.
$l = (l_1, l_2, l_3)$ is computed from the intersection of 2 sets of imaged parallel lines.
Metric / Similarity Rectification: remove affine distortion
The image of the circular points (absolute points) $I, J$ is specified
$I = (1, i, 0), J = (1, -i, 0)$
Every circle intersects $l_{\infin}$ at the circular points.
The dual to the circular points: $C_{\infin}^* = IJ^T + JI^T = \begin{bmatrix}1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 0\end{bmatrix}$
-
$C_{\infin}^*$ has 4 Dof
5 conic - 1 $det(C_{\infin}^*) = 0$
-
$l_{\infin}$ is the null vector of $C_{\infin}^*$
-
$cos\theta = {l^T C_{\infin}^m \over \sqrt{(l^TC_{\infin}^l)(m^TC_{\infin}^*m)}}$
$C_{\infin}^{‘}=(H_PH_AH_S)C_{\infin}^(H_PH_AH_S)^T=(H_PH_A)C_{\infin}^(H_AH_P)^T=U C_{\infin}^U^T$ , the recitifying projectivity is $H=U$
$C_{\infin}^{‘’}=H_p^{-1}C_{\infin}^{‘}H_p^{-T}=H_AC_{\infin}^H_A^T$ is the image of $C_{\infin}^$ after removal of projective distortion.
Metric rectification of an affinely rectified image
Suppose $l’, m’$ in the affinely rectified image correspond to an orthogonal line pair $l, m$ on the world plane.
$(l^TH_A^{-1})H_AC_{\infin}^H_A^T(H_A^{-T}m^T) = l’C_{\infin}^{‘‘}m’= 0$
We can compute $C_{\infin}^*{‘’}$ and hence $H_A$ from 2 pairs of orthogonal lines.
$(l_1’, l_2’, l_3’)\begin{bmatrix}KK^T & 0 \ 0^T & 0\end{bmatrix}(m_1’, m_2’, m_3’)^T=0$, where we write $S_{2\times2}=KK^T$ with 3 independent elements.
The orthogonality constraint can be written as: $(l_1’m_1’, l_1’m_2’+l_2’m_1’, l_2’m_2’)s = 0$, where $s=(s_{11}, s_{12}, s_{22})^T$ is $S$ written as a 3-vector.
Metric rectification of perspective image of the plane (not affinely rectified)
$C_{\infin}^{‘}=(H_PH_A)C_{\infin}^(H_AH_P)^T=\begin{bmatrix}KK^T & KK^Tv \ v^TKK^T & v^TKK^Tv\end{bmatrix}$
$(l_1’m_1’, (l_1’m_2’+l_2’m_1’)/2, (l_1’m_3’+l_3’m_1’)/2, (l_2’m_3’+l_3’m_2’)/2, l_3’m_3’)c = 0$, where $c = (a, b, c, d, e, f)^T$ is $C_{\infin}^*{‘}$ written as a 6-vector.
We can compute $C_{\infin}^*{‘}$ and hence $H_PH_A$ from 5 pairs of orthogonal lines.
The Pole-Polar Relationship
Polar Line: $l=Cx$
Point $x$ doesn’t line on C implies $x^TCx≠0$
If the point $x$ is on $C$ then the polar is the tangent line to the conic at $x$.
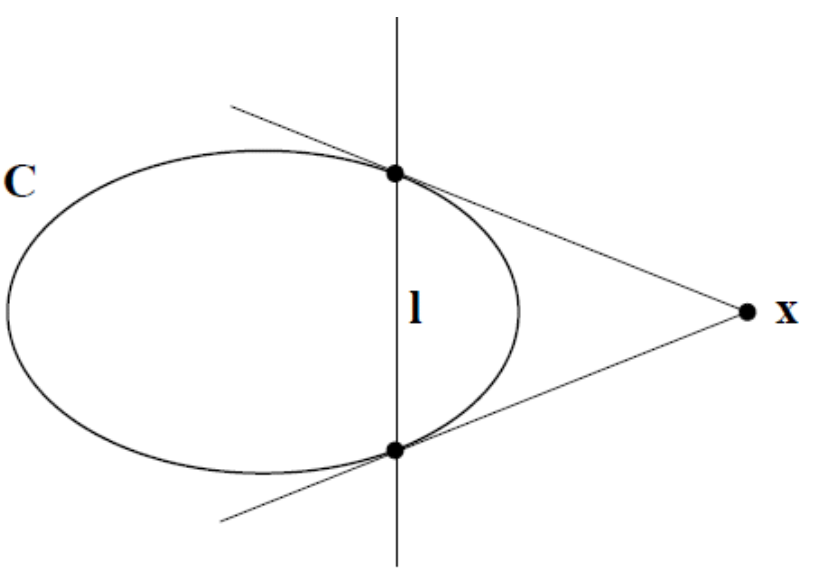
Conjugate Points $y^TCx=0$
The conjugacy relation is symmetric: If $x$ is on the polar of $y$ then $y$ is on the polar of $x$.
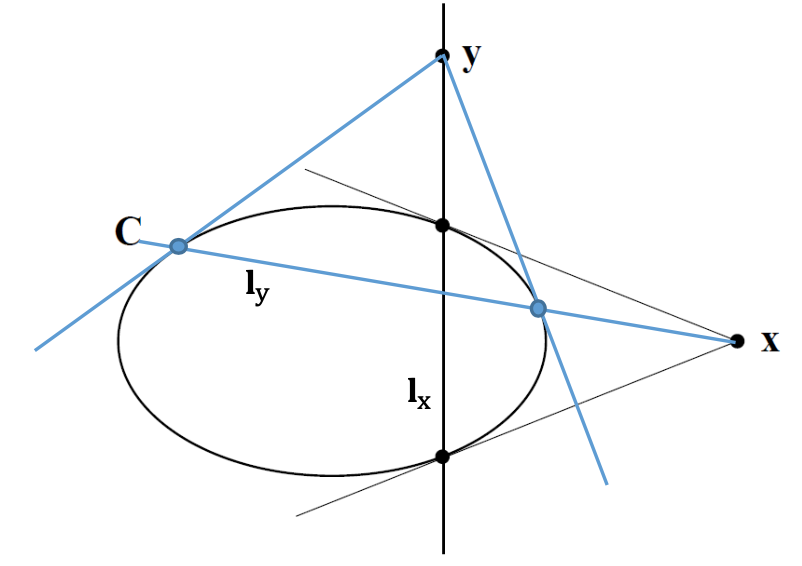
dual: $l^TC^*m=0$
Polar Plane $\pi=QX$
- $Q$ is non-singular and $X$ is outside the quadric.
- If $X$ lies on $Q$, then $QX$ is the tangent plane to $Q$ at $X$.