Consensus

Goal

Termination: All nodes (that have not failed) eventually decide
Agreement: All nodes that decide should decide on the same value
Validity: If all nodes have the same initial input, that value should be the only possible decision value. Otherwise nodes are allowed to decide on anything (except that they still need to satisfy the Agreement requirement)

Consensus with Node Crash Failures/Synchronous

Failure model

Nodes may experience crash failure
Communication channels are reliable

Timing model

Synchronous: Message delay has a known upper bound x, and node processing delay has a known upper bound y
Implies the possibility of accurate failure detection

Inter-locked rounds

Where in each round,

Every process sends one message to every other process
Every process receives one message from every other process
Every process does some local computation

Dummy messages can be used.

Messages sent during a round is received during that round

Accurate failure detection

via Clocks with Bounded Error

Each process first performs a send (taking time no more that $t_1$).
Message propagation and receiving the message no more than $t_2$.
Local processing no more than $t_3$.

Bounded error: Consider an example where the clock on a certain process is twice as fast as an accurate clock.

To compensate

Everyone sets the timer duration to be $2(t_1+t_2+t_3)$

To start the next round at the same time

If a process receives a round 2 message while in round 1, it immediately start round 2
Everyone sets the timer duration to be $2((t_1+t_2+t_3) +t_1+t_2)$, since the round starting time at different processes may differ by $t_1+t_2$.

Protocol

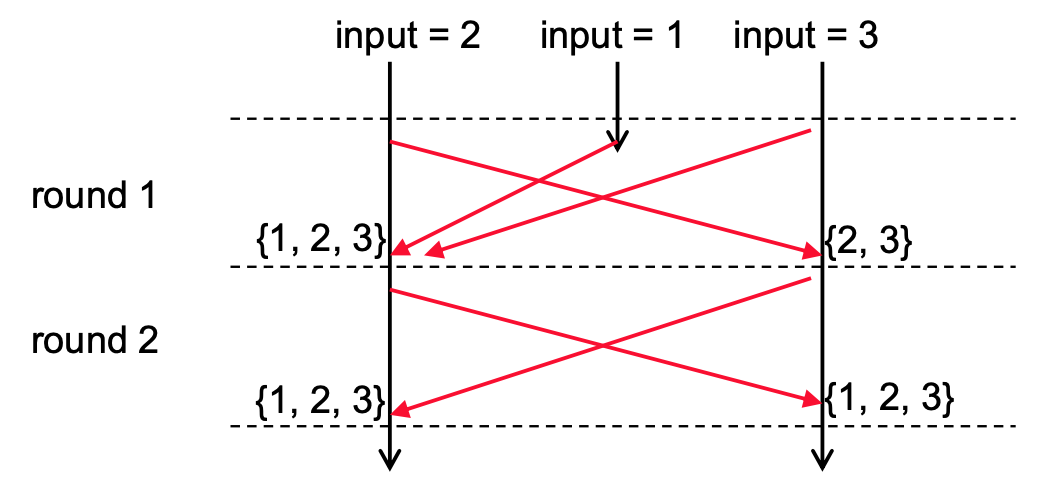
Need $f+1$ rounds to tolerate $f$ failures. $f$ needs to be input.

Proof

nonfaulty: A node is nonfaulty if it has not crashed by the end of round $r$

good: A round is good if there is no node failure during that round

With $f+1$ round and $f$ failures, there must be at least on good round.

At the end of any good round $r$, all non-faulty nodes during round $r$ have the same $S$

Suppose $r$ is a good round, and consider any round $t$ after round $r$. During round $t$, the value of $S$ on any non-faulty nodes does not change.

All nonfaulty processes at round $f+1$ will have the same $S$

Consensus with Link Failures (Coordinated Attack Problem)

Failure model

Nodes do not fail
Communication channels may fail - may drop arbitrary (unbounded) number of messages

Timing model

Synchronous: Message delay has a known upper bound x, and node processing delay has a known upper bound y

It is impossible to reach the above goal using a deterministic algorithm, since the communication channel can drop all messages.

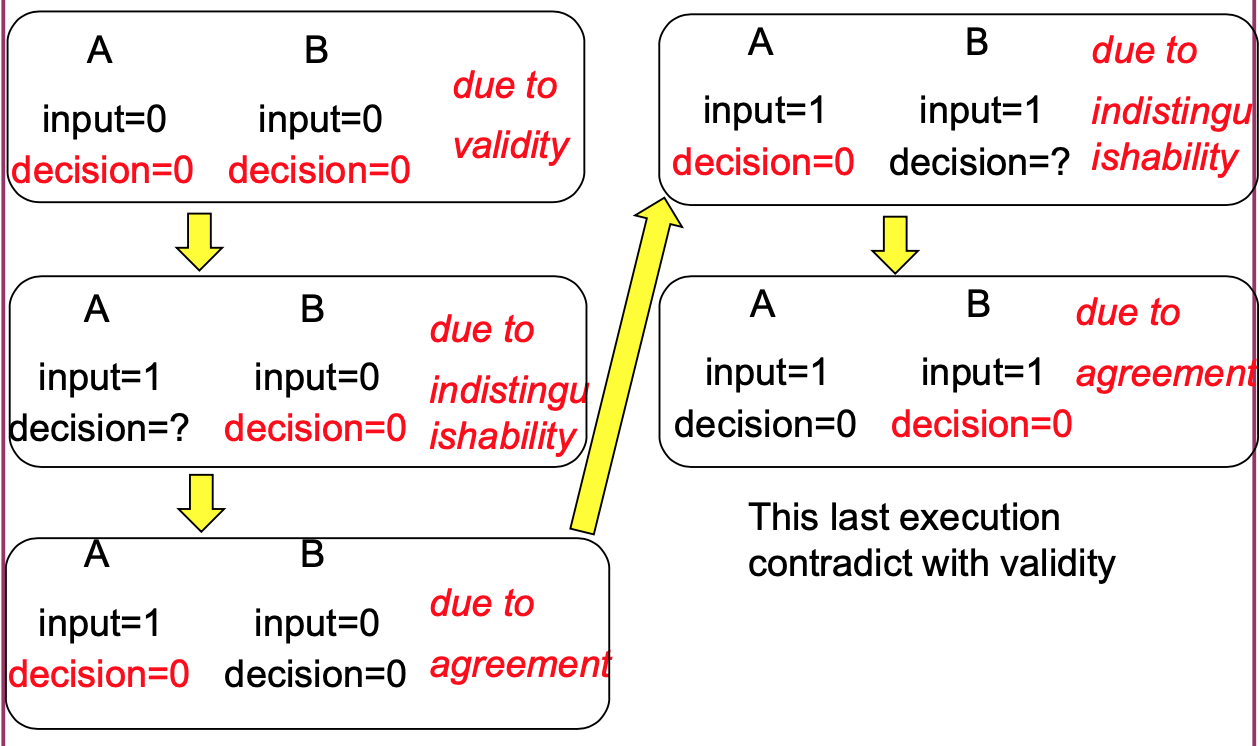
Weakened Validity

Assuming input either 0 or 1,

If all nodes start with 0, decision should be 0
If all nodes start with 1 and no message is lost throughout the execution, decision should be 1
Otherwise nodes are allowed to decide on anything

It is still impossible to reach the above weakened goal using a deterministic algorithm

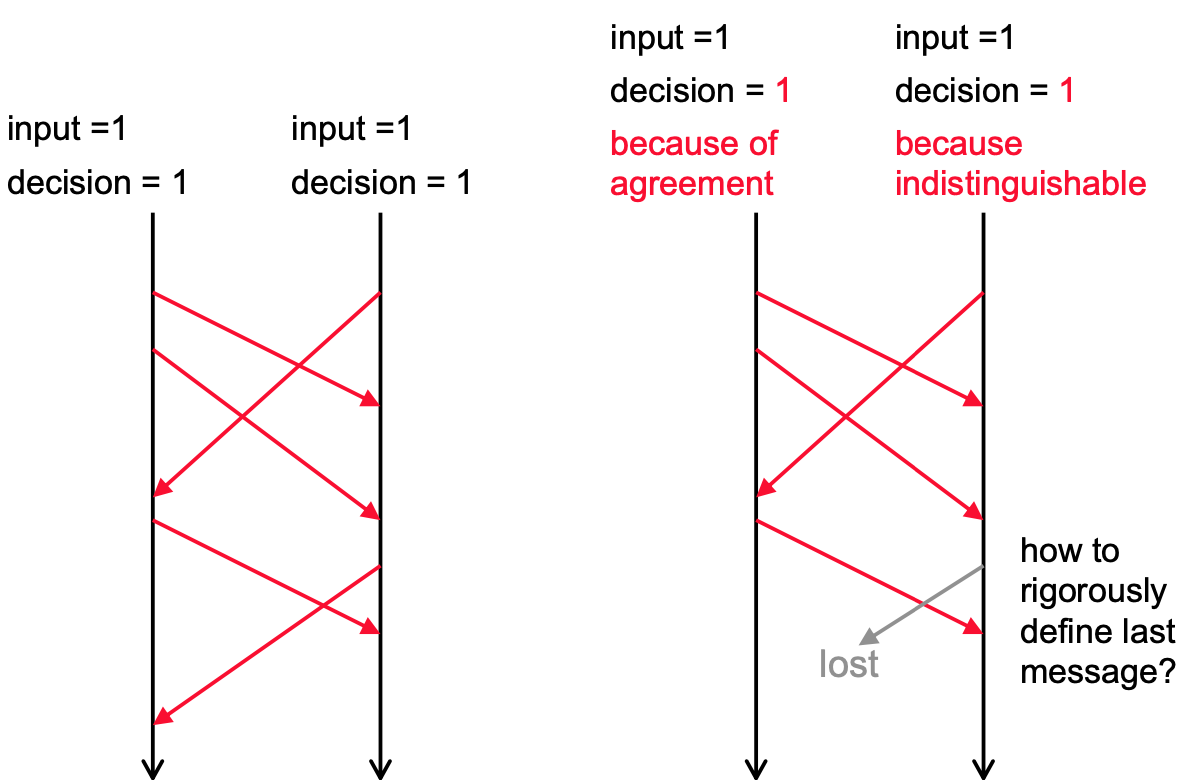
Can remove the last message until all messages are dropped, while decision is still 1.

Allowing Limited Disagreement

Goal

Termination: All nodes eventually decide
Agreement: All nodes decide on the same value with probability of $(1 – error_prob)$
Validity:
- If all nodes start with 0, decision should be 0
- If all nodes start with 1 and no message is lost throughout the execution, decision should be 1
- Otherwise nodes are allowed to decide on anything

A Randomized Algorithm

Algorithm has a predetermined number ($r$) of rounds
P1 picks a random integer $bar \in [1…r]$ at the beginning
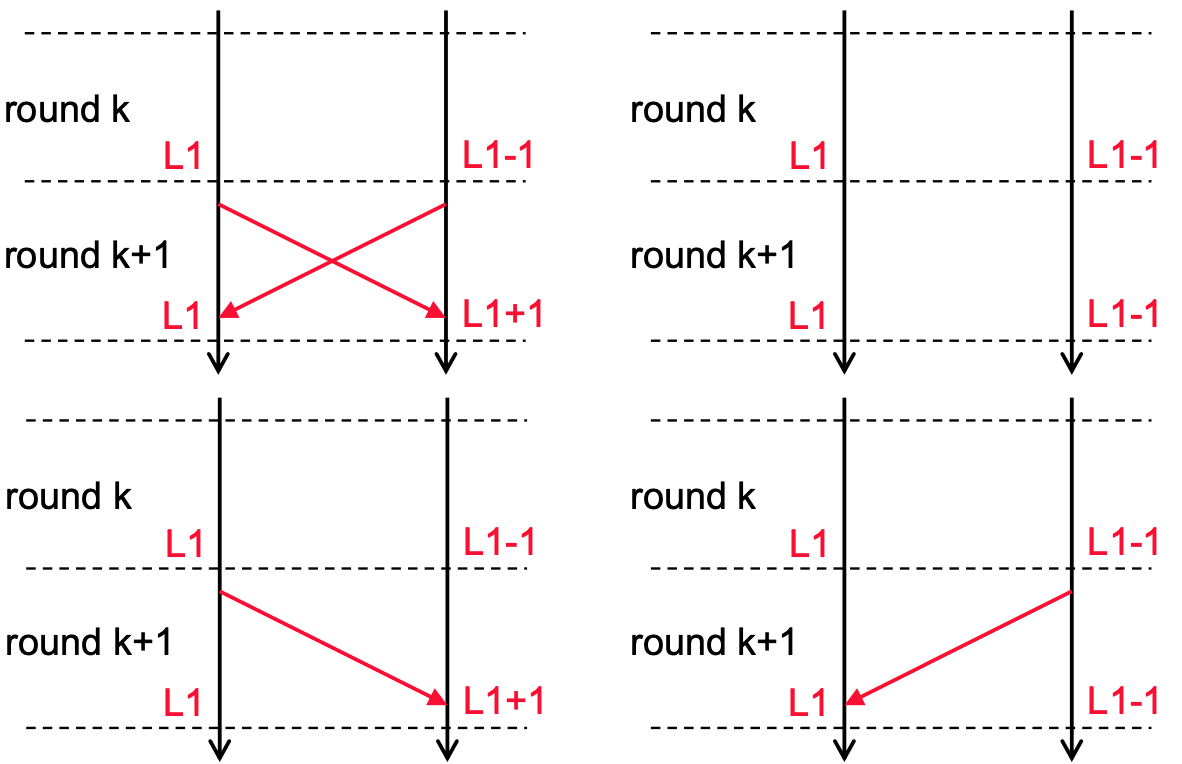
The protocol allows P1 and P2 to each maintain a level variable (L1 and L2), such that
- Level is influenced by the adversary
- L1 and L2 can differ by at most 1
bar, input and current level attached on all messages
Upon P2 receiving a msg with L1 attached: L2 = L1 + 1, L1 maintained similarly

Lemma: L1 and L2 never decreases in any round, and at the end of any round, L1 and L2 differ by at most 1.

Decision Rule

At the end of the r rounds, P1 decides on 1 iff
- P1 knows that P1’s input and P2’s input are both 1, and
- L1 ≥ bar
i.e. P1 will decide on 0 if it does not see P2’s input
At the end of the r rounds, P2 decides on 1 iff
- P2 knows that P1’s input and P2’s input are both 1, and
- P2 knows bar, and
- L2 ≥ bar
i.e. P2 will decide on 0 if it does not see P1’s input OR it does not see bar

When does error occur?

Case 1: P1 see P2’s input, but P2 does not see P1’s input or bar.

L1 = 1, L2 = 0. Error occurs when bar = 1.

Case 2: P2 see P1’s input and bar, but P1 does not see P2’s input.

L1 = 0, L2 = 1. Error occurs when bar = 1.

Case 3: P1 see P2’s input, and P2 see P1’s input and bar.

Lmax = max(L1, L2). Error occurs when bar = Lmax.

Correctness Proof

Termination: $r$ rounds

Validity:

If all nodes start with 0, decision should be 0
If all nodes start with 1 and no message is lost throughout the execution, decision should be 1
- If no messages are lost, then L1=L2=r $\rightarrow$ P1 and P2 will decide on 1
Otherwise nodes are allowed to decide on anything

Aggreement: With $1-{1\over r}$ probability

Consensus with Node Crash Failures/Asynchronous

Failure model

Nodes may experience crash failures
Communication channels are reliable

Timing model

Asynchronous: Processs delay and message delay are finite but unbounded.

The protocol is unable to accurately detect node failure.

FLP Impossibility Theorem

The distributed consensus problem under the asynchronous communication model is impossible to solve even with a single node crash failure.

Formalisms for FLP Theorem

Goal: To abstract the execution of any possible deterministic protocol

Each process has some local state and two special variables: input $\in$ {0, 1}, decision $\in$ {null, 0, 1}
Each communication channel has some state: Messages “on the fly”
The message system captures the state of all communication channels.
- {(p, m) message m is on the fly to process p}
- All messages are distinct (include sender, receiver, sequence number)
Send = add(p, m) to the message system
Receive invoked by process p =
- Remove (p, m) from message system and return m
- Leave the message system unchanged and return null
  - No message on the fly has been sent to p
  - There are messages sent to p but are still on the fly
Global state of the system include all process states and message system state
A step in a protocol takes the system from one global state to another:
- receive a message m (m can be null)
- based on p’s local state and m, send an arbitrary but finite number of messages
- based on p’s local state and m, change p’s local state to some new state
These actions are done by a single process p
(p, m) is an event, it can fully describe each step given a global state.
- Events are inputs to the state machine that cause state transitions
- An event can be aplied to global state if either m is null or (p, m) is in the message system

The execution of any protocol can be abstracted to be an infinite sequence of events

A schedule $\delta$ is a sequence of events that captures the execution of some protocol

$\delta$ can be applied to G if the events can be applied to G in the order in $\delta$
G’=$\delta$(G). Need to be careful when we write $\delta(G)$, since $\delta$ may or may not be applied to G

Given a consensus protocol A, a global state G2 is reachable from G1 if there exists a schedule $\delta$ such that G2=$\delta$(G1).

It is impossible to reach the above goal using a deterministic algorithm, since the communication channel can drop all messages

Agreement: No reachable global state from any initial state has more than one decision.

Validity: If all nodes have the same initial input, they should all decide on that.

Termination: Eventually all processes decide.

Formalisms for Asynchronous System and Failures

Processes have unbounded but finite delay
- A nonfaulty process tasks infinite number of steps.
- A faulty process tasks a finite number of steps.
Messages have unbounded but finite delay
At most one faulty process

Proof for FLP Theorem

General Proof technique:

Act as the adversary to defeat the consensus protocol
Can pick which message to deliver (message propagation delay) and which process will take the next step (node processing delay)
Goal is to prevent the protocol from deciding

Classification of Global States

G is 0-valent if 0 is the only possible decision reachable from G
G is 1-valent if 1 is the only possible decision reachable from G
G is bivalent if it is not univalent (1-valent or 1-valent)

Lemma 1: For any protocol A, there exists a bivalent initial state

Prove by Contradiction

Consider n+1 initial states with input vector being (0,0,…,0), (1,0,…,0), (1,1,0,…,0),…,(1,1,…,1)

Assumpting: no bivalent state.

There must be two adjacent initial states S0 and S1 where S0 is 0-valent and S1 is 1-valent.
S0 and S1 differ by the input to a single process p.
Consider an execution starting from S0 where p fails at the very beginning.
- If the decision is 1, then S0 is not 0-valent.
- If the decision is 0, then S1 is not 1-valent.

Lemma 2: Let $\delta$1 and $\delta$2 be two schedules s.t. the set of process executing steps in $\delta$1 are disjoint from the set that execute steps in $\delta$2. Then for any G that $\delta$1 and $\delta$2 can both be applied, we have $\delta$1($\delta$2(G)) = $\delta$2($\delta$1(G))

Induction

Induction base k=1: e1(e2(G)) = e2(e1(G)). Suppose e1=(p1, m1), e2=(p2, m2).

Since e1 can be applied to G, it means either m1 is null or (p1, m1) is in the message system. The same is for e2.
Because p1≠p2, e1 can be applied to e2(G) and e2 can be applied to e1(G).
Let G1=e1(e2(G)) and G2=e2(e1(G)). Then the state of the message system is the same. The states of all processes are the same. G1=G2.

Inductive hypothesis: k=max(

$\delta$1

$\delta$2

)

Induction step k+1:

Case 1:

$\delta$1

=k+1,

$\delta$2

≤k

Suppose the first event in $\delta$1 is e and $\delta$1=($\delta$

e) where

$\delta$

=k. Then $\delta$1($\delta$2(G))=$\delta$(e($\delta$2(G)))=$\delta$($\delta$2(e(G)))=$\delta$2($\delta$(e(G)))=$\delta$2($\delta$1(G))

Case 2:

$\delta$1

≤k,

$\delta$2

=k+1

Case 3:

$\delta$1

=k+1,

$\delta$2

=k+1

Suppose the first event in $\delta$2 is e and $\delta$2=($\delta$

e) where

$\delta$

=k. Then $\delta$1($\delta$2(G))=$\delta$1($\delta$(e(G)))=$\delta$($\delta$1(e(G)))=$\delta$(e($\delta$1(G)))=$\delta$2($\delta$1(G))

Lemma 3: Let e=(p,m) be an event that can be applied to G. Let W be the set of global states that is reachable from G without applying e, then e can be applied to any state in W.

Case 1: m is null.

Null message can be applied to any state.

Case 2: (p,m) is in the message system of G

Other events cannot remove (p,m) from the message system, therefore (p,m) is still in the message system of W. (p,m) can be applied to any state in W.

Lemma 4: Let G be a bivalent state, and e=(p,m) is any event that can be applied to G. Let W be the set of global states that is reachable from G (G is in W) without applying e, and V=e(W). Then V contains a bivalent state.

Prove by Contradiction: Assume V does not contain a bivalent state.

Claim 1: There must be a 0-valent state F, s.t. F=$\delta$(G) and $\delta$ contains the event e.

G is bivalent thus we must have a 0-valent state G0 reachable from G when G0=$\delta$1(G).
Case 1: $\delta$1 contains event e. F=G0 and $\delta$=$\delta$1.
Case 2: $\delta$1 does not contain event e. F=e(G0), $\delta$=(e $\delta$1). Because G0 is 0-valent, F must be 0-valent as well.

Claim 2: There must be a 0-valent state G0 in V.

Consider the prefix $\delta’$ of $\delta$ as defined in Claim 1, whose last event is e. Let G0=$\delta’$(G) $\in$ V
Because V does not contain bivalent states and the 0-valent state F=$\delta$(G) is reachable from G0, G0 must be 0-valent.

Claim 3: There must be 1-valent state G1 in V.

Claim 4: There must be F0 and F1 in W, s.t. e(F0) is 0-valent, e(F1) is 1-valent, and either F1=d(F0) or F0=d(F1), i.e. F0 and F1 are neighbors.

Let G0 be a 0-valent state in V and G1 be a 1-valent state in V.

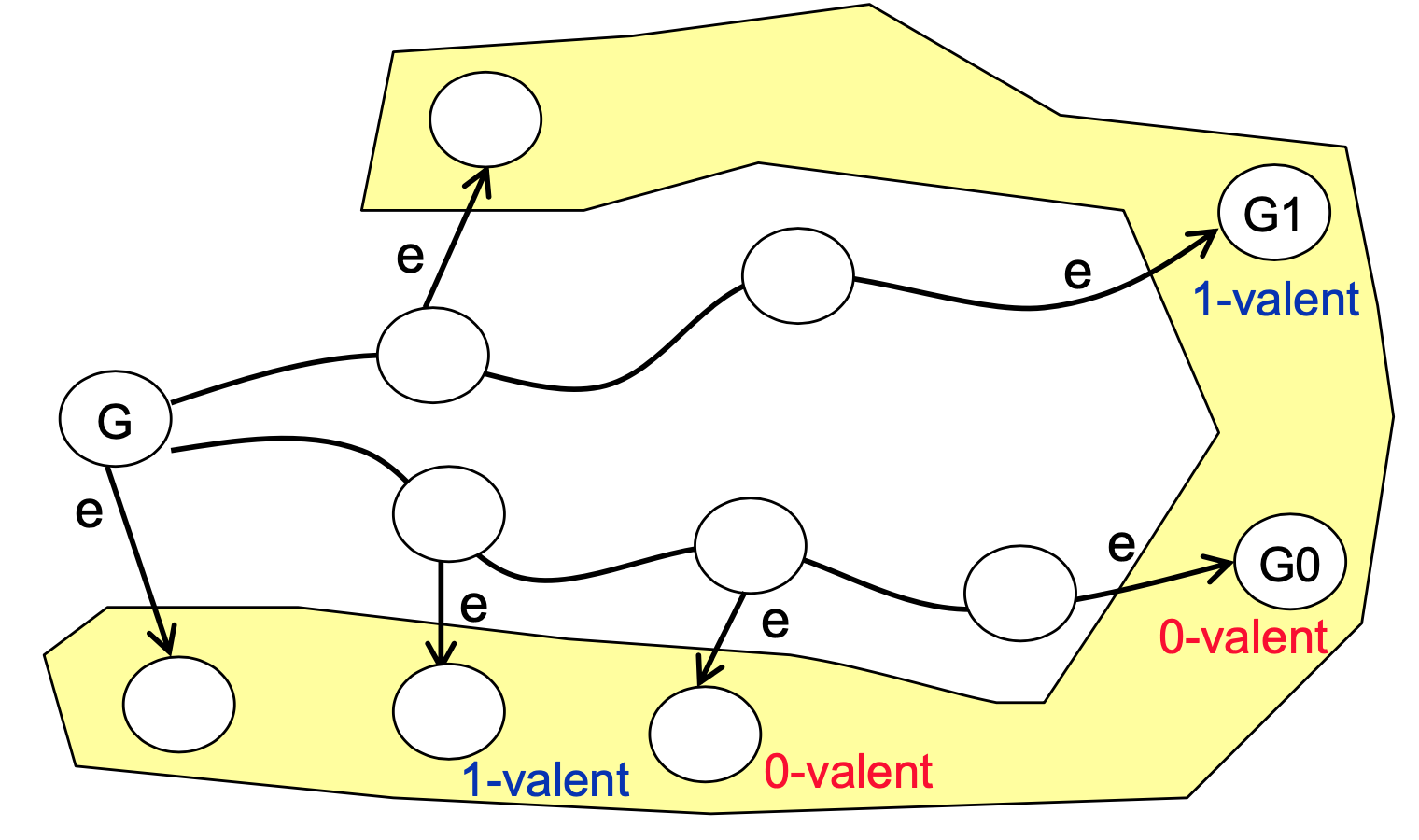
Lemma 4

Consider F0 and F1 in W, s.t. e(F0)=G0 is 0-valent, e(F1)=G1 is 1-valent, assume F1=d(F0) (Lemma 4)
e and d must occur on the same process p because otherwise G1=e(F1)=e(d(F0))=d(e(F0))=d(G0), which contradicts.
Consider all possible executions starting from state F0. By termination requirement and to tolerate one process failure, there must be an execution where
- some process decides
  
  and
- process p doesn’t execute any steps
Let the state immediately after some process decides be T where T=$\delta$(F0) and $\delta$ does not contain any step by p.
We have e(T)=e($\delta$(F0))=$\delta$(e(F0))=$\delta$(G0) which is 0-valent (Lemma 2)
We also have e(d(T))=e(d($\delta$(F0)))=$\delta$(e(d(F0)))=$\delta$(e(F1))=$\delta$(G1) which is 1-valent (Point 2, Lemma 2)
But some process has already decide in T. Regardless of whether the decision is 0 or 1, agreement can be violated. Contradiction.

Proof for FLP Theorem

Start with a bivalent state and try to keep in a bivalent state.

Processes take steps in round-robin fashion. Imagine that it is process p’s turn.
If the message system contain no messages for p, let e=(p,null). Otherwise consider the oldest message m destined to p, and let e=(p,m).
Let G be the current state. Execute (p,m) if e(G) is bivalent.
Otherwise find a finite length $\delta$ that does not contain e and e($\delta$(G)) is bivalent (Lemma 4). Apply $\delta$ then apply e.
The system will always be in a bivalent state.

Consensus with Node Byzantine Failures/Synchronous

Failure model

Nodes may experience byzantine failures (to defeat the protocol)
Communication channels are reliable

Timing model

Synchronous

$n$: the total number of processes

$f$: the number of possible byzantine failures

If $n≤3f$, then byzantine consensus problem cannot be solved.

Protocol

We will develop a protocol for $n≥4f+1$.

Process $i$ is the coordinator for phase $i$.
Coordinator sends a proposal to all processes.
- Each phase has a coordinator round to do this.
- If coordinator is nonfaulty, all processes sees the proposal-consensus.
- A phase is a deciding phase if the coordinator is nonfaulty.
With at most $f$ failures and $f+1$ phases, at least one phase is deciding phase.
After a deciding phase, all non-faulty processes have the same value.
To avoid a faulty coordinator to overrule the outcome of a deciding phase, do not listen to the coordinator if
- I see a lot of identical values from other processes
- Each phase will also have a all-to-all broadcast round

V[1..n]=0, V[i]=my input;
for (k=1; k≤f+1; k++) {
	// all-to-all broadcase round
	send V[i] to all processes;
	set V[1..n] to be the n values received;
	if (value x occurs > (n/2) times in V) proposal=x;
	else proposal=0;
	
	// coordinator round
	if (k==i) send proposal to all;
	reveive coordinatorProposal from the coordinator;
	
	// decide whether to listen to the coordinator
	if (value y occurs > (n/2+f) times in V) V[i]=y;
	else V[i]=coordinatorProposal;
}
decide on V[i];

Lemma 1: If all non-faulty process $P_i$ have $V[i]=y$ at the beginning of phase $k$, then this remains true at the end of phase $k$.

$n-f > n/2 +f$ when $n>4f$
if (value y occurs > (n/2+f) times in V) V[i]=y;

Lemma 2: If the coordinator in phase $k$ is nonfaulty, then all nonfaulty processes $P_i$ have the same $V[i]$ at the end of phase $k$.

Case 1: Coordinator has proposal = $x$; ($x$ must be unique on coordinator)

On coordinator: $x$ appears ($> n/2$) times in $V$ $\Rightarrow$ ($>n/2-f$) must be from nonfaulty processes
On any other process: $x$ appears ($>n/2-f$) times in $V$ $\Rightarrow$ Impossible for $y$ to appear ($>n/2+f$) times in $V$
if (value x occurs > (n/2) times in V) proposal=x;
if (value y occurs > (n/2+f) times in V) V[i]=y;

Case 2: Coordinator has proposal=$0$;

On coordinator: no value $x$ appears ($>n/2$) times $V$
- $n$ is even, and half of the processes has a value of $1$ and half are $0$
On any other process: Impossible for $y$ to appear ($>n/2+f$) times in $V$
- Because there are only $f$ faulty processes

Correctness Proof

Termination: $f+1$ phases

Validity: Lemma 1

Agreement:

With $f+1$ phases, at least one of them is a deciding phase.
Immediately after the deciding phase, all non-faulty processes $P_i$ have the same $V[i]$ (Lemma 2)
In the following phases, $V[i]$ on non-faulty processes $P_i$ does not change (Lemma 1)

PREVIOUSRectification

NEXTLeader Election